Kardioide

Kardioiden er en glatt kurve med en spiss.

Kardioide er en plan og lukket kurve med en spiss. Formen kan minne om et hjerte slik at den ofte blir omtalt som hjertekurven.

Den er en episykloide som er generert av et punkt på en sirkel som ruller på en annen, stasjonær sirkel med samme radius. Av denne grunn kan den også betraktes som et spesialtilfelle av Pascals snegle.

En matematisk beskrivelse av kardioiden er enklest ved bruk av polarkoordinater (r,θ). Den er da gitt ved ligningen

$r(\theta )=2a(1-\cos \theta )$

hvor parameteren a bestemmer dens størrelse. Med disse koordinatene har den spissen i origo Mal:Nowrap, mens punktet med størst avstand fra origo er i Mal:Nowrap.

Evoluten til kardioiden er en mindre kardioide. Kurven beskriver også formen til den største delen av Mandelbrot-mengden når man ser bort fra dens fraktale detaljer.

Matematisk beskrivelse

Kardioiden er en episykloide hvor den rullende sirkelen har samme radius som den stasjonære.

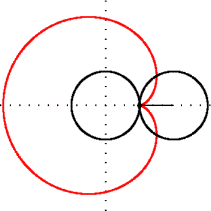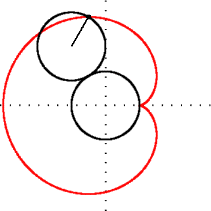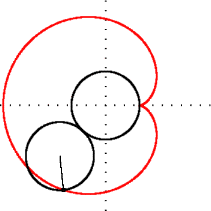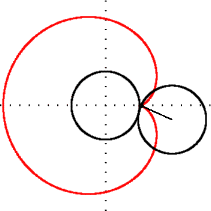
Fra dens fremstilling i polarkoordinater kan man finne en ekvivalent beskrivelse i kartesiske koordinater Mal:Nowrap og Mal:Nowrap. Det gir

$x(\theta )=2a(1-\cos \theta )\cos \theta =a(2\cos \theta -1-\cos 2\theta )$

$y(\theta )=2a(1-\cos \theta )\sin \theta =a(2\sin \theta -\sin 2\theta )$

som viser at den er en episykloide av to sirkler med samme radius a hvorav den ene ruller utenpå den andre. I motsetning til standardfremstillingen av episykloiden, er denne kardioiden forskjøvet et stykke a langs den negative x-aksen.

En implisitt ligning for kurven i dette koordinatsystemet kan utledes fra observasjonen at $r^2+2ax=r(r+2a\cos \theta )=2ar.$ Da finner man ligningen

$(x^2+y^2+2ax{)}^2=4a^2(x^2+y^2)$

når man benytter at $r^2=x^2+y^2.$ Den viser at kardioiden er en kurve av fjerde grad.

Buelengde

I polarkoordinater er den differensielle buelengden til en plan kurve gitt som $ds=(d{r}^2+r^{2}d{\theta }^2{)}^{1/2}$. Hele omkretsen til kardioiden er dermed

$s=\underset{0}{\overset{2\pi }{\int }}d\theta (r^2+(dr/d\theta {)}^2{)}^{1/2}$

Nå er

$\begin{array}{cc}{r}^2+(dr/d\theta {)}^2& =4a^2(1-2\cos \theta +{\cos }^2\theta +{\sin }^2\theta )\\ & =16a^2{\sin }^2\theta /2\end{array}$

slik at omkretsen blir

$s=4a\underset{0}{\overset{2\pi }{\int }}d\theta \sin \theta /2=16a$.

Areal

På samme måte er arealet til kardioden gitt ved flateintegralet

$\begin{array}{cc}A& =\underset{0}{\overset{r}{\int }}dr\underset{0}{\overset{2\pi }{\int }}rd\theta =\frac{1}{2}\underset{0}{\overset{2\pi }{\int }}{r}^{2}d\theta \\ & =2a^2\underset{0}{\overset{2\pi }{\int }}d\theta (1-2\cos \theta +{\cos }^2\theta )=6\pi a^2.\end{array}$

Geometriske egenskaper

Kardioiden som omhyllingskurve for en skare sirkler. Den gitte sirkelen er antydet i blått.

Kardioiden opptrer i mange forskjellige sammenhenger. For eksempel er den omhyllingskurven til en skare sirkler som har sitt sentrum på en sirkel og som går gjennom et gitt punkt på sirkelen. Velges den faste sirkel å ha radius r = 1 og sentrum i punktet (-1, 0), vil hvert punkt på den være gitt som

$x_c=-1+\cos \theta ,y_c=\sin \theta$

avhengig av vinkelen θ. Hvis nå origo (0, 0) velges som det faste punktet på sirkelen, vil dette ha den kvadrerte avstanden

$r_c^2=x_c^2+y_c^2=(-1+\cos \theta {)}^2+{\sin }^2\theta =2-2\cos \theta$

til sirkelsenteret. Den gitte skaren av sirkler er gitt ved ligningen $(x-x_c{)}^2+(y-y_c{)}^2=r_c^2$ eller $F(x,y,\theta )=0$ hvor

$F(x,y,\theta )=x^2+y^2+2x(1-\cos \theta )-2y\sin \theta$

For at to sirkler i denne skaren med nesten samme verdi av parameteren θ skal tangere den samme omhyllingskurven, må Mal:Nowrap = 0. Nå er Mal:Nowrap slik at denne betingelsen er oppfylt når punktene (x,y) på omhyllingskurven kan skrives på formen Mal:Nowrap og Mal:Nowrap. Den ukjente størrelsen r  bestemmes fra Mal:Nowrap som gir de to løsningene r = 0 og Mal:Nowrap. Denne siste fremstiller en kardioide med størrelse Mal:Nowrap som tilsvarer radius til den gitte sirkelen.

Evolute

Evoluten i grønt til en kardioide er en ny kardioide som er 1/3 av den opprinnelige. Krumningssenteret til hvert punkt P ligger i et tilsvarende punkt M på evoluten.

Punkter x på evoluten til kardioiden r = 4a sin²θ/2 (cosθ, sinθ) er definert ved formelen Mal:Nowrap hvor ρ er krumningsradius til kurven og n er dens normerte normal. Begge disse størrelsene kan finnes fra tangentvektoren $𝐓=d𝐫/d\theta$ med komponenter

$𝐓=(\frac{dx}{d\theta },\frac{dy}{d\theta })=4a\sin \frac{\theta }{2}(\cos \frac{\theta }{2}\cos \theta -\sin \frac{\theta }{2}\sin \theta ,\sin \frac{\theta }{2}\cos \theta +\cos \frac{\theta }{2}\sin \theta )$

Den normerte tangentvektoren er derfor

$𝐭=(\cos \frac{3\theta }{2},\sin \frac{3\theta }{2})$

når man benytter de trigonometriske identitetene for sinus og cosinus for en sum av to vinkler. Den normerte normalvektoren er derfor $𝐧=(-\sin (3\theta /2),\cos (3\theta /2)).$

Kardioidens krumningsradius ρ finnes nå direkte fra Frenets første formel Mal:Nowrap = Mal:Nowrap. Det betyr at Mal:Nowrap hvor Mal:Nowrap er kjent fra dens buelengde.

Dermed er x-koordinatene til evoluten Mal:Nowrap gitt ved

$\begin{array}{cc}x& =4a{\sin }^2\frac{\theta }{2}\cos \theta -\frac{8}{3}a\sin \frac{\theta }{2}\sin \frac{3\theta }{2}\\ & =\frac{4}{3}a{\sin }^2\frac{\theta }{2}\cos \theta -\frac{4}{3}a{\sin }^2\theta =-\frac{4}{3}a+\frac{4}{3}a{\cos }^2\frac{\theta }{2}\cos \theta \end{array}$

På samme vis finnes y-koordinatene å være $y=\frac{4}{3}a{\cos }^2\frac{\theta }{2}\sin \theta .$ Evoluten til kardioiden er derfor en ny kardiode som 1/3 av den opprinnelige, speilvendt om y-aksen og forskjøvet (4/3)a langs den negative x-aksen. Før denne forskyvningen er den gitt ved den polare ligningen Mal:Nowrap som tydeliggjør speilingen om y-aksen.

Litteratur

• E. H. Lockwood, A Book of Curves, Cambridge University Press, England (1967). ISBN 0-5210-4444-8.

Eksterne lenker

• Stackexchange, Why does the boundary of the Mandelbrot set contain a cardioid?, argument basert på eksistens av fikspunkt