Maxwell-relasjon

Maxwells relasjoner slik de ble publisert i 1871.

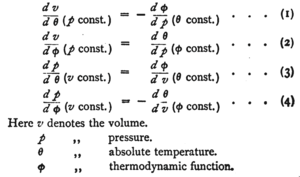
Maxwell-relasjon er en ligning mellom førstederiverte av forskjellige variable som benyttes i beskrivelsen av et termodynamisk system. Den er en direkte konsekvens av symmetrien til den andrederiverte av et termodynamisk potensial som avhenger av de samme variable. Da det finnes flere ulike slike potensial, finnes det et sett av forskjellige Maxwell-relasjoner. De kan benyttes til å forbinde forskjellige matematiske resultat i termodynamikken med målbare størrelser som er av praktisk beydning.

Disse relasjonen ble funnet av James Clerk Maxwell og offentliggjort som en fotnote i hans lærebok Theory of Heat  som kom ut i 1871. De er av like stor betydning i dag som den gang.

Utledning

Den fundamentale ligningen i termodynamikken er U = U(S,V) som gir den indre energien U  til et system som funksjon av dets entropi S  og volume V. Sammenligner man funksjonens differensial

$dU={\left(\frac{\partial U}{\partial S}\right)}_{V}dS+{\left(\frac{\partial U}{\partial V}\right)}_{S}dV,$

med den termodynamiske identiteten Mal:Nowrap kan systemets temperatur T  og trykk P  bestemmes fra

$T={\left(\frac{\partial U}{\partial S}\right)}_V,P=-{\left(\frac{\partial U}{\partial V}\right)}_S$

To partielle derivasjoner etter hverandre kan byttes om slik at man har symmetrien ${\partial }^{2}U/\partial S\partial V={\partial }^{2}U/\partial V\partial S.$ Her har den nå den matematiske konsekvensen

${\left(\frac{\partial T}{\partial V}\right)}_S=-{\left(\frac{\partial P}{\partial S}\right)}_V$

som er den første Maxwell-relasjonen.

Flere relasjoner

De energetiske forholdene til et termodynamisk system kan uttrykkes ved flere andre funksjoner enn den indre energien U. Disse kalles for termodynamiske potensial og kan finnes fra energien U(S,V) ved Legendre-transformasjoner. På den måten defineres systemets entalpi som Mal:Nowrap slik at Mal:Nowrap. Funksjonen Mal:Nowrap har nå differensialet

$dH={\left(\frac{\partial H}{\partial S}\right)}_{P}dS+{\left(\frac{\partial H}{\partial P}\right)}_{S}dP,$

De konjugerte variable til S  og P  er dermed

$T={\left(\frac{\partial H}{\partial S}\right)}_P,V={\left(\frac{\partial H}{\partial P}\right)}_S$

og gir den nye Maxwell-relasjonen

${\left(\frac{\partial T}{\partial P}\right)}_S={\left(\frac{\partial V}{\partial S}\right)}_P$

På samme vis vil Helmholtz fri energi U - TS  være en funksjon F = F(T,V) som gir Maxwell-relasjonen

${\left(\frac{\partial S}{\partial V}\right)}_T={\left(\frac{\partial P}{\partial T}\right)}_V,$

mens Gibbs fri energi H - TS  er en funksjon G = G(T,P) med Maxwell-relasjonen

${\left(\frac{\partial S}{\partial P}\right)}_T=-{\left(\frac{\partial V}{\partial T}\right)}_P.$

Dette er i alt fire relasjoner og er de samme som inngikk i Maxwells opprinnelige arbeid hvor han benyttet en noe annen notasjon.

Åpne system

Når systemet kan utveksle partikler med omgivelsene, har det ikke lenger et bestemt antall partikler N. Den indre energien er da en funksjon U(S,V,N) slik at den termodynamiske identiteten må utvides til Mal:Nowrap hvor μ  er systemets kjemiske potensial. Basert på den indre energien oppstår det nå to nye Maxwell-relasjoner,

${\left(\frac{\partial T}{\partial N}\right)}_{SV}={\left(\frac{\partial \mu }{\partial S}\right)}_{VN},{\left(\frac{\partial P}{\partial N}\right)}_{SV}=-{\left(\frac{\partial \mu }{\partial V}\right)}_{SN}.$

Tilsvarende relasjoner vil fremkomme fra de andre, termodynamiske potensialene når man lar dem variere med partikkeltallet og det kjemiske potensialet. Helmholtz fri energi er da Mal:Nowrap = F(T,V,N), mens Gibbs fri energi Mal:Nowrap = G(T,P,N) = Nμ(T,P).

For åpne system kan man i gitte situasjoner også benytte Landau fri energi. Den fremkommer ved en Legendre-transformasjon hvor antallet N  i Helmholtz fri energi erstattes med det kjemiske potensialet, Mal:Nowrap = Ω(T,V,μ) = - PV. Dette potensialet gir opphav til tre nye Maxwell-relasjoner.

Eksterne lenker

• Oulu Universitet, Thermodynamic potentials, lecture notes